銀河を見かけの形によって分類する形態分類の一つ。 ハッブル(E. Hubble)が基本概念を1926年の論文に発表し、1936年の著書(The Realm of the Nebulae)で、それを可視化する有名な音叉図とともに紹介した。銀河は 楕円銀河(E)と渦巻銀河(S)に大別され、 さらに渦巻銀河は通常の渦巻銀河(S)と 中心に棒状構造のある棒渦巻銀河(SB)と の2つの系列に分類される。 渦巻銀河はほぼ回転楕円体である中心のバルジと 円盤(ディスク)とから構成されるが、 バルジ成分の割合や渦巻腕の巻き込みの強さなどから添え字a, b, cなどをつけてより詳細に分類される。 ハッブルは、楕円銀河より扁平だが渦巻腕も棒状構造もない、 楕円銀河と渦巻銀河の中間の形態をレンズ状銀河( S0:エスゼロ)として仮想的に導入したが、 その後観測によってその存在が立証された。 さらに、数%の割合で存在する対称性の悪い銀河を不規則銀河(Irr)としたが、対称性が悪い原因が異なる複数種の銀河が混在することが今ではわかっている。 渦巻銀河とレンズ状銀河を合わせて円盤銀河ということがある。
ハッブルは彼の形態分類を例示する図を作成した。そこでは先に述べたように、渦巻銀河を正面向きで(円盤面と垂直な方向から)見た際のバルジの回転対称性に応じて、対称性が悪く細長い棒状構造を持つ棒渦巻銀河(SB)とほぼ円形に見える(狭義の)渦巻銀河(SまたはSAの分類記号が用いられる)に2分しており、レンズ状銀河はこの2系列の分岐点に位置づけられている。この図は音楽で使う音叉を横にしたような図式となるためハッブルの音叉図と呼ばれる。音叉図で表される系列をハッブル系列という。
音叉図で左にあるほど早期型、右にあるほど晩期型といわれる。これは当時、音叉図上で銀河が左から右へ進化するとの考えがあったためである。それが間違いであることはすぐに明らかになったが、「早期」、「晩期」という用語法、さらに 早期型銀河や晩期型銀河という分類用語は現在でも用いられている。ただし、「早期型」や「晩期型」は相対的に用いられる場合も多く、どれをそう呼ぶかが明確に定義されているわけではな。このため、使う人や文脈によって指す形態分類の範囲が異なる場合があり、注意が必要である。
ハッブル分類をさらに細分化したものがドゥ・ボークルール分類である。 この分類で導入された形態型指数と、両分類の対応を表に示す。
ガスのはぎ取り(銀河の)を参照。
楕円型の2階微分方程式、たとえば、
$$\frac{\partial^2 \phi(x,y)}{\partial x^2} + \frac{\partial^2 \phi(x,y)}{\partial y^2}=\rho(x,y)$$
に対して、境界条件が、境界 $D$ での値を用いて、$\phi(x,y)|_{D}=f(x,y)$ のように与えられている場合をいう。ノイマン問題も参照。
収差のある光学系での点像分布関数は焦点の近くではほぼ円形で、光軸上の位置によって分布半径が変わる。その半径が最小となる位置の円を最小錯乱円と呼ぶ。
スターバーストを参照。
銀河団を、最も明るい銀河とそれ以外の銀河との明るさの対比に基づいて分類したもの。この分類を提唱したバウツ(L.P. Bautz)とモルガン(W.W. Morgan)の名による。I型は銀河団中心に1つのcD銀河があるもの、II型は銀河団中心に卓越した銀河(cDまたは巨大楕円銀河)が複数個あるもの、III型は銀河団中心に卓越した銀河が見られないものをそれぞれ表す。cD銀河は銀河団の重力ポテンシャルの底に成長する巨大銀河であるため、その有無は銀河団の力学的進化段階を表すともいえる。
デカルト座標系 $(x, y, z)$ を用いた計算格子。
銀河合体のことであるが、特に、小銀河が大銀河に合体して飲み込まれることをいう。力学摩擦によって大きな銀河に落下した小さな銀河が、強い潮汐力によって引き裂かれて壊され、大銀河へと吸収同化され、一体化すること。
偏微分方程式を差分法を用いて解くとき、細かい格子が必要な部分だけに選択的に細かい計算格子を用い、それ以外の部分には粗い計算格子を用いる方法。AMR法と省略されることが多い。解適合格子と呼ばれることもある。細かい格子が必要になる部分は解の構造に依存するので、解の時間発展に合わせて計算格子を動的に貼りかえる。適合格子細分化法を用いると、少ない格子点数で実効的に高い解像度を得ることができる。衝撃波を細かい格子で分解したり、形成される小さな天体を高解像度で分解したりするときに有効な方法である。
適合格子細分化法に用いる計算格子はいくつかの種類に分類される。天体物理学のシミュレーションでは、構造格子を用いたブロック構造格子(図参照)と、構造格子を持たない直交非構造格子を採用することが多い。
レンズや鏡の形状により生じる光学収差には数学的な考察から、球面収差、コマ収差、非点収差、像面湾曲、歪曲という5つの基本的なパターンがあることが1857年のザイデル(L. von Seidel)の研究で示された。波面収差Wを瞳座標(ρ, θ)と入射角 $\alpha$ で多項式展開すると、3次までの展開式は
$$ W = B\rho^4 + F\alpha\rho^3 \cos\theta + C\alpha^2 \rho^2 \cos^2\theta + D\alpha^2\rho^2 + E\alpha^3\rho \cos\theta $$
となる。この5つの項をザイデルの五収差と呼ぶ。B, F, C, D, Eをそれぞれ球面収差係数、コマ収差係数、非点収差係数、像面湾曲係数、歪曲係数と呼ぶ。
アンテナのビームパターンのうち、主ビームの広がりの外側にできる、同心円状ないし局所的に感度が高まっている部分。主ビームとの境界には明確な定義はないが、通例、中心から離れる方向に対して最初の極小値となる範囲で囲まれた部分の外側をいう。広がった天体や込み入った天体群を観測する場合、主ビームで検出した電波とサイドローブで検出した電波とは区別が付かないので、天体望遠鏡としてはサイドローブの感度レベルが低いことは極めて重要である。サイドローブは、焦点に集まる電磁波が有限の広さの面から得られることに原因があり、0にすることは原理的に不可能である。サイドローブを軽減するには、主鏡面の照射パターンを外縁部に近づくにつれて次第に弱くすることや副鏡とその支柱によるブロッキングを減らしたりなくすことなどが効果的である。なお、可視光や近赤外線ではこのような調整は通常行わず、サイドローブに相当する回折環やスパイダー像と呼ばれる十字型のパターンが星像に発生する。
銀河を見かけの形によって分類する形態分類の一つ。ドゥ・ボークルール(G. de Vaucouleurs)が提唱した。ハッブル分類をより詳細にしたもので、改訂ハッブル分類とも呼ばれる。渦巻銀河に対して、ハッブル分類のScの後ろにさらに晩期型のSdとSmを追加し、不規則銀河のI型をIm、II型をI0(アイゼロ)とした。早期型から晩期型への系列とは別の次元で、棒構造の多様性を表すために、SA(棒なし)、SAB(中間)、SB(棒あり)のタイプを導入し、また渦巻構造の多様性を表すためにr(リング)、rs(中間)、s(スパイラル)のサブタイプを導入した。
改訂ハッブル分類は右図(上)に示すようなサツマイモに似た分類立体で表現される。分類立体の中心軸がハッブル系列に対応し、左端の楕円銀河から右に向かってレンズ状銀河、渦巻銀河、不規則銀河と次第に晩期型が配置される。中心軸に垂直な断面には、棒構造と渦巻構造の多様性が展開される。ドゥ・ボークルールは、中心軸に沿った系列が銀河の主要な物理的性質を反映し、それに垂直な断面は微細な力学的多様性を表すと考え、中心軸に沿う系列に形態型指数 T を割り当て、形態を物理量のように定量的に扱えるようにした。分類型と形態型指数 T の対応関係は、ハッブル分類との対応も含めて下の表に示されている。
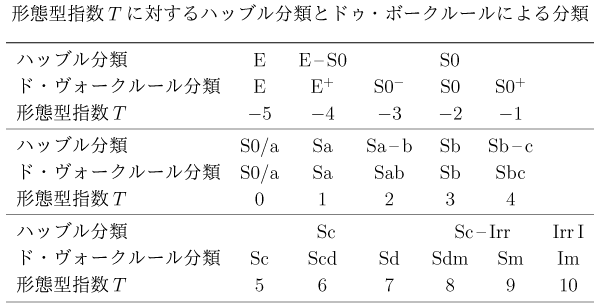
出典:土居守「銀河の種類と形態分類」、シリーズ現代日本の天文学第4巻、谷口・岡村・祖父江編『銀河I』1.1節 1.1表(日本評論社)
銀河は宇宙の膨張にともなって、銀河までの距離に応じて、より遠い銀河ほど大きな速度でわれわれから後退しているように見える(ハッブル-ルメートルの法則)。この宇宙膨張による見かけの速度(ハッブル流)以外の速度成分を特異運動と呼ぶ。銀河の周囲に銀河群や銀河団などが存在する場合、それによる重力によって銀河の局所的な運動が生ずる。この特異運動の大きさを特異速度といい、数百から1000 km s-1程度にもなることがある。1980年代初めには、宇宙マイクロ波背景放射(CMB)の観測から、局所銀河群は宇宙全体の静止系と考えられるCMBに対して約600 km s-1の速度で運動していることが明らかになった。1986年に、この運動が、おとめ座銀河団への落ち込み運動と、うみへびーケンタウルス座銀河団が、局所超銀河団を引き寄せている運動の合成で説明されるとして、局所超銀河団より大規模な領域で銀河が揃った運動をしていることが指摘され、それ以後超銀河団より大きなスケールでの大規模な銀河の特異運動(bulk motionあるいはstreaming motionと呼ばれる)が活発に研究されるようになった。ラニアケア超銀河団も参照。
中性子星の最深部や宇宙の極く初期のように超高温、高密度の極限世界では、第1世代(アップ・ダウンクォーク、電子など)のみならず、第2世代(チャーム・ストレンジクォーク、ミューオンなど)、第3世代(トップ・ボトムクォーク、タウ粒子など)の素粒子やその複合体が現れる可能性がある。
たとえばケーオン(K中間子)はストレンジクォーク1個と反アップクォーク1個からなる中間子である。ストレンジクォークを含むバリオンをハイペロンと呼び、ハイペロンを含む原子核をハイペロン核という。
形態分類の体系に合わない形態を持つ銀河の総称。伝統的には目視検査により形態分類を行った研究者が、分類体系に当てはまらないと判定した銀河を特異銀河とした。したがって、特異銀河の明確な定義は存在しないし、準拠する形態分類によっても判断が異なる場合もある。アープ(H. Arp;1927-2013)が作成した『アープアトラス』(Atlas of Peculiar Galaxies)には338個の特異銀河の写真が収められている。反対方向に延びる2本の細長い尾や、リング構造、弧状のシェルなどが特異銀河に特徴的な構造である。これらの構造は、銀河同士の衝突時の重力的相互作用(潮汐力など)の結果、銀河の形が歪められたり壊されたりすることによって生ずると考えられており、数値シミュレーションによってもよく再現されている。
多数の銀河に対する銀河画像から抽出した定量的なパラメータで、従来の形態分類に相当する体系をつくるさまざまな研究がおこなわれている。定量パラメータの空間では「正常な銀河(分類形態によく合致する銀河)」と「特異銀河」は連続的につながっており、両者の線引きは主観的なものにならざるを得ないとする研究もある。
天文学では観測や測定に際して、対象としている天体や機器から発生する電磁波を信号と呼び、それ以外に由来する電磁波を雑音と呼ぶ。英語のままノイズと呼ぶこともある。したがって、放射過程や電磁波の特徴という点では信号と雑音の違いがない場合も多い。たとえば、天体からの電磁波を信号と考える場合、それ自身の揺らぎや地球大気または検出器が生じる放射とそのゆらぎはすべて雑音として扱う。雑音は、その物理学的起源や周波数特性の違いによって分類可能で、熱雑音、量子雑音、フリッカ雑音、白色雑音、ピンクノイズなどが知られている。なお、実際の観測では天体からの信号に対する雑音の強さが問題となるため、途中で信号の増幅や減衰がある場合には、増幅や減衰が現れる前段での強さに換算して評価することが多く、これを入力換算雑音や等価雑音と呼ぶ。システム雑音も参照。
特異運動(銀河の)を参照。
望遠鏡の架台の一種。赤道儀は、1軸を地球の自転軸に平行に設定する。この軸を極軸と呼ぶ。極軸に垂直なもう一方の軸を赤緯軸と呼ぶ。赤道儀では、天体の日周運動の速度(すなわち地球の自転速度に等しい逆向き速度)で極軸周りに鏡筒を東から西に回転させることで、日周運動する天体を追尾することができる。よって、極軸周りの定速回転機構があれば天体追尾が可能となる。また、赤道儀の主焦点やカセグレン焦点では、天体追尾に伴って視野回転が生じない。このような利点を持つため、望遠鏡架台として広く採用されている。
赤道儀は、制御系が簡便になる反面、機械構造的には弱い。重力方向に対して傾斜した極軸を持ち、天体観測時には一般に赤緯軸も重力に対して傾く。これらの軸周りに十分な剛性を持たせるために、軸の支持構造は重く頑丈とする必要があり、望遠鏡が大型化すると現実的な構造物を建造することが難しくなってしまう。このため、近年では大型望遠鏡架台として赤道儀が用いられることはない。世界最大の赤道儀式光学望遠鏡は1948年に完成したパロマー天文台にある口径5 mのヘール望遠鏡である。世界最大の赤道儀式電波望遠鏡はNRAOの43m電波望遠鏡。経緯台も参照。
弧状衝撃波を参照。
天の川銀河(銀河系)の最大の球状星団より大きいきわめて表面輝度の高い矮小銀河。典型的な大きさは、球状星団が2-3パーセク(約10光年)であるのに対し数10パーセク(約100光年)、また明るさは、球状星団が太陽の100万倍程度以下であるのに対して、1000万倍程度である。1999年にろ座銀河団で発見されたが、その後他の銀河団や、銀河団以外の環境にも存在することがわかった。銀河と球状星団の間をつなぐ天体であるが、その形成過程はまだよくわかっていない。
