オーストラリアのニューサウスウェールズ州サイディングスプリングにあるオーストラリア国立大学(ANU)が運用する天文台。口径3.9 mのアングロオーストラリア望遠鏡(AAT)、UKシュミット望遠鏡(UKST)、口径2.3 m望遠鏡および口径1.3 mの全自動望遠鏡SkyMapper等の望遠鏡がある。
ホームページ:http://www.sidingspringobservatory.com.au/
(ANU) https://rsaa.anu.edu.au/observatories/siding-spring-observatory
ガウス(Carl Friedrich Gauss;1777-1855)はドイツの数学者、物理学者、天文学者。数論から測地学、光学と広範な研究を行ない、19世紀最大の数学者といわれる。ニーダーザクセン州ブラウンシュヴァイクで貧しい労働者の子として生まれたが、幼少から神童の誉れ高く、7歳にして1から100までの級数が101の50組の和であることを示したというエピソードがある。1798年にゲッティンゲン大学を卒業、20歳代前半までに、正17角形の作図法、楕円関数の二重周期性、最小自乗法、代数学の基本定理の証明、整数論など、画期的研究成果をあげた。
1801年に発見された小惑星ケレスと第2の小惑星パラスの軌道決定、および軌道決定理論は天文学上の大きな業績である。1807年にはゲッティンゲン大学教授と同天文台長を務め、測地学、地磁気学でも多くの優れた研究成果を残した。その後、新天文台建設(1816年完成)に邁進するとともに、数列、特殊関数、積分法、統計などの数学研究を行なった。1818年には実際に測量に従事し、1820年代は測地学に進んだ。1800年代から非ユークリッド幾何学に興味をいだき、1816年に平行線の話を書いた。1828年、微分幾何学の本を出版。1830年代は物理学に興味をいだき、ポテンシャルの概念を導入した。これは彼の物理学への最も大きな貢献とされる。また、地磁気や磁気の研究も行なった。磁気誘導の単位「ガウス」や「ガウスの誤差法則」、「ガウスの最小二自乗法」などに名を残す。また、国際数学連合(IMU)により、数学の応用に対して「ガウス賞」が2002年に設けられている。
参考:https://mathshistory.st-andrews.ac.uk/Biographies/Gauss/
黄道面(黄道を参照)を基準面として定義した天球の座標系。この座標系における経度を黄経、緯度を黄緯と呼ぶ。黄緯0°が黄道面であり、黄緯±90°は黄道の極である。黄道の北極を北黄極(North Ecliptic Pole(NEP))。南の極を南黄極(South Ecliptic Pole(SEP))と呼ぶ。黄経の原点は春分点の方向にとり、黄道に沿って東回りに角度を測る。太陽系の惑星や小天体は黄道面近くに多く分布しているから、太陽系天体の運動を考えるのに便利な座標系といえる。
黄道傾斜角をεとすると、赤道座標系(赤経 α (アルファ)、赤緯 δ)と黄道座標系(黄経 λ、黄緯 β)の変換は、以下のようになる。
$$
\begin{pmatrix}
\cos \beta \cos \lambda \\
\cos \beta \sin \lambda \\
\sin \beta \\
\end{pmatrix}
=
R_1(\varepsilon)
\begin{pmatrix}
\cos \delta \cos \alpha \\
\cos \delta \sin \alpha \\
\sin \delta \\
\end{pmatrix}
$$
ここでR1(ε)はx軸周りの回転行列で
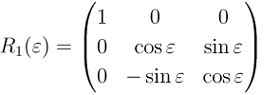
である。
ちなみに、NEPの赤道座標は(18h00m00.s, +66°33'38."6)(J2000)、また銀河座標は(96.°3840, +29.°8114)(J2000) である。また、銀河面(天の川銀河(銀河系)の赤道面)と黄道面の関係は図のようになる。
天球上の座標系を定めるために選ばれた天体の座標が掲載されているものを位置星表と呼ぶが、その中でも最も精度の高い星表を基本星表と呼ぶ。FK3カタログ、FK4カタログ、FK5カタログなどがあった。
1998年に国際天文準拠系(ICRS)が採用されてからは、それを具現化するICRF等のカタログが基本星表の役割を担っている。
コンピュータ上に築かれた仮想的な天文台。バーチャル天文台(VO)とも呼ぶ。計算機の中に蓄えられたデータを観測された宇宙と見なし、それをいろいろな角度から解析(観測)するという概念から名づけられている。現在、世界中で電波からガンマ線に至るまで広い波長域における天体観測データが、データアーカイブとして構築され、インターネット上で公開されている。VOは、こうした世界中の天文アーカイブデータを有機的に結合し、共通化されたインターフェースを用いてさまざまな天体データを横断的に検索、閲覧、収集、解析できることを目指している。国立天文台にはJVO (Japanese Virtual Observatory) がある。各国の主要天文学研究機関はそれぞれ独自のVOを構築しているが、それらを連携した世界規模のVOの構築も進展している。
ホームページ(国際VO):http://www.ivoa.net/
ホームページ(日本VO):http://jvo.nao.ac.jp/index.html
アクリル板に写真乳剤(臭化銀など)を両面に塗布したもので、荷電粒子が入射すると乳剤中の物質を電離して電子を作り、その電子が銀イオンを引き付けるため、現像すると荷電粒子が通過した飛跡を銀粒子の集まりとして見ることができる。普通の写真乾板に比べ臭化銀粒子は小さく、濃度は高く、乳剤層を厚くすることにより高感度になっている。エマルションチェンバーも参照。
黄道座標系を参照。
アメリカ航空宇宙局(NASA)とヨーロッパ宇宙機関(ESA)が共同で開発して、1997年に打ち上げた土星探査機。当初は、小惑星彗星探査機(Comet Rendezvous Asteroid Flyby(CRAF))と同じプラットフォームを使い同時に開発をする計画であったが、CRAFは中止になり、その予算はカッシーニに向けられた。2000年に木星によるスイングバイを行い、ガリレオ探査機と木星磁気圏の共同観測を行った。2004年6月30日に土星周回軌道に投入され、12月にタイタン着陸船ホイヘンスを切り離した。ホイヘンスは2005年1月14日にタイタン表面に着陸した。降下中の大気、カメラのデータや、表面の観測データや画像を、カッシーニ経由で地球へ送信した。降下中のカメラの画像から、メタンの雨によると思われる河川地形を発見した。タイタンの極域にメタンの雲、湖が存在することをカッシーニは観測している。カッシーニの成果のなかでも最大のものは、エンセラダスから氷とガスのプリュームが吹き出していることを発見し、その成分を調べたことである。また土星のリング中に複雑な構造があることも明らかにしている。2011年時点で、ほぼすべての観測機器が順調に作動しており、2017年までの延長運用を行ったが、2017年9月15日に土星大気に突入して、観測を終了した。
ホームページ:
https://solarsystem.nasa.gov/missions/cassini/overview/
https://www.nasa.gov/mission_pages/cassini/main/index.html
黄道を参照。
国際協力を通じてあらゆる側面から天文学の発展を図ることを目的として、1919年に設立された非政府の世界組織。国際科学会議(ISC、2017年以前はICSU)に属する40の国際学術団体の一つである。天文学者を代表する国の機関が加盟するナショナルメンバーと、個人として加入する個人メンバーから構成される。2018年にジュニアメンバーの制度が作られた。日本は設立の翌年、1920年にナショナルメンバーとして加盟した。2019年時点で、ナショナルメンバーは82か国(地域を含む)、個人会員は13556名(うちジュニアメンバー348名)である。このうち日本人の会員は767名で、アメリカ、フランスに次いで第3位である(以下イギリス、中国、ドイツと続く)。IAUの研究活動は、研究分野ごとに設置された9つの部会(Division)と、その下にある、より専門化された35のテーマ別委員会(Commission)および50あまりの作業部会(Working Group)で行われる。総会は3年に1度、世界各国を回って開かれる。日本では1997年に京都で開催された。2006年にプラハで開催された総会では、惑星の定義が採択され、冥王星を惑星ではなく準惑星という新しい天体種族に分類したことが話題となった(その後、冥王星型天体という新しい種族名が決められた)。日本での対応については以下の日本学術会議の「対外報告」を参照のこと。
2009年にユネスコと行った「世界天文年(International Year of Astronomy)」の活動が成功したことを受けて、それ以降教育普及関連の活動を活発に行っている。2009年のリオデジャネイロで開催された総会で、2010-2020年の10年戦略計画「発展途上国のための天文学」(2012年の北京総会で「発展のための天文学」に改名)が採択され、それを受けて2011年にはケープタウンの南アフリカ天文台に「社会発展のための天文学推進室(OAD: Office of Astronomy for Development)」が開設された。さらに続いて、2012年には日本の三鷹の国立天文台に「国際普及室(OAO: Office for Astronomy Outreach)」が、2015年にはオスロのノルウェー科学アカデミーに「若手支援室( OYA: Office for Young Astronomers)」が設置された。2018年にウィーンで開催された総会で、「発展のための天文学」を引き継ぎ更に発展させる ‘Strategic Plan 2020-2030’(2020-2030年の戦略計画)が採択され、2019年11月に「天文教育支援室(OAE: Office of Astronomy for Education)」が、ドイツのハイデルベルグにある「天文の家(Haus der Astronomie)」に設置された。学校教育における天文学の利用は「2020-2030年の戦略計画」の目標の一つである。
このようなIAUの活動に資するため、市民に知っておいて欲しい天文学の基本概念をまとめた ‘Big Ideas in Astronomy-A Proposed Definition of Astronomy Literacy’ や天文学を行う上で開発された技術が多くの分野に応用され市民生活にも役立てられていることを解説した ‘From Medicine to Wi-Fi; Technical Applications of Astronomy to Society’ などの資料が出版されている。またウィーン総会では、宇宙膨張に関する「ハッブルの法則」を今後は「ハッブル-ルメートルの法則」と呼ぶことを推奨する決議が提案され、2018年10月に会員の投票で採択された。日本での対応については以下の日本学術会議の「提言」を参照のこと。
IAUはまた、スミソニアン天文台(ハーバード大学天文台も参照)が運営する天文電報中央局の、新天体に関する天文電報(IAU Circular)の発行も支援している。
ホームページ:http://www.iau.org/
惑星の定義に関連する日本学術会議の「対外報告」(2007年)
http://www.scj.go.jp/ja/info/kohyo/pdf/kohyo-20-t35-1.pdf
http://www.scj.go.jp/ja/info/kohyo/pdf/kohyo-20-t39-3.pdf
ハッブル-ルメートルの法則に関する決議についての日本学術会議の「提言」(2018年):
http://www.scj.go.jp/ja/info/kohyo/pdf/kohyo-24-t273-1.pdf
Strategic Plan 2020-2030
https://www.iau.org/administration/about/strategic_plan/ (英文原版:日本語版)
日本語版は、日本天文教育普及研究会のホームページからもダウンロードできる
https://tenkyo.net/activity/iau-publications/iau_strategic_2019_jp/ (日本語版)
Big Ideas in Astronomy-A Proposed Definition of Astronomy Literacy(英語版)
https://www.iau.org/news/announcements/detail/ann19029/
ビッグアイデア-天文学の主要概念-天文学リテラシーの提案(日本語版)
https://tenkyo.net/activity/iau-publications/big_ideas2020/
From Medicine to Wi-Fi; Technical Applications of Astronomy to Society(英語版)
https://www.iau.org/public/images/detail/ann19022a/
天文学の技術と私たちの生活 医療からWi-Fiまで(日本語版)
https://tenkyo.net/activity/iau-publications/from_medicine_to_wi-fi/
1980年代初めに岐阜県神岡鉱山の地下1000mの場所に建設された水チェレンコフ検出器。3000t の水タンクに948本の直径0.5m光電子増倍管を1m間隔で内面に取り付けた装置であり、荷電粒子が水中の光の速度よりも速く運動した際に発生するチェレンコフ光をとらえる。天体ニュートリノ観測装置としては、SN1987Aからの超新星爆発に伴うニュートリノや太陽ニュートリノ欠損を検出し、建設を主導した小柴昌俊東京大学名誉教授は2002年のノーベル物理学賞を受賞した。本来の目的が陽子崩壊を検出する装置(Kamioka Nucleon Decay Experiment)だったため、この名前になった。1996年からは性能を大きく向上した後継機スーパーカミオカンデに引き継がれた。ニュートリノ天文学も参照。
変光星、新星、超新星、小惑星など光度が変化する天体の光度を時間の関数として表した図のこと。英語をそのまま用いて「ライトカーブ」と言うことも多い。一般に、縦軸に天体の明るさ(「等級」)を取り、横軸に時刻を取って表す。周期的な変化を示すものは、時間の代わりに位相をとって表すことが多い。天体の種類によって光度曲線にはさまざまな特徴が見られる。
光度曲線(超新星の)、光度曲線(変光星の)、光度曲線(小惑星の)を参照。
日本の天文学研究(主に地上からの観測と理論)の中心研究機関の一つ。
正式名称は、大学共同利用機関法人自然科学研究機構国立天文台。前身の東京天文台は東京大学の附置研究所であった。1988年に東京大学を離れて文部省直轄の大学共同利用機関国立天文台へと改組された。2004年4月の国立大学法人化に伴い、自然科学研究機構の中の一つの研究所となった。
本部は東京都三鷹市にある。ハワイのマウナケア国際天文台で口径8.2 mのすばる望遠鏡を、また、南米チリでは、国際共同でアルマ望遠鏡を運用するほか、東京大学などと共同で口径10 mのサブミリ波望遠鏡ASTEも運用している。現在、国際共同でハワイマウナケア山頂に口径30 mの光赤外線望遠鏡TMTを建設中である。国内でも野辺山電波天文台の45 m電波望遠鏡などいくつかの装置を運用している。
ホームページ:https://www.nao.ac.jp/
国立天文台 紹介ビデオ 2013
提供:NAOJ https://youtu.be/s8AUzf0ofEQ
メートル条約に基づいて1875年に設立された国際的な研究機関で、その活動と予算は条約加盟国(2021年時点で57か国)の合意に基づいて決められる(日本は1885年にメートル条約に加盟)。フランス語の名称(Bureau International des Poids et Mesures)の略号で BIPMと呼ばれることもある。世界中で一つの一貫した単位系(国際単位系(SI))を実現するための基礎を提供することを目的としている。国際原子時(TAI)の維持を含むさまざまな活動を行っている。
パリ郊外のセーヌ河沿いにあって、かつて長さと質量の基準であった国際メートル原器と国際キログラム原器はここの原器庫で保管され厳重に管理されていた。2018年11月の第26回総会でSI単位の定義が大幅に改訂され、2019年から新しい定義が施行されてSI基本単位の中で原器により定義されるものはなくなった。
ホームページ:https://www.bipm.org/en/
1675年にイギリス国王チャールズ2世によってロンドンの郊外グリニッジに設立された天文台。グリニッジ天文台と呼ばれることが多い。大航海時代にあった当時、外洋における船の位置を天文観測から測定し、航海術の進歩の基礎とすることも重要な目的であった。王室から雇用された初代台長はフラムスティード(J. Flamsteed:1646-1719)で、以降台長は王室付天文学者(Astronomer Royal)の称号を与えられる慣例が1971年まで続き、イギリス天文学の中心となった(1972年以降はAstronomer Royalの称号は名誉称号となり天文台長とは必ずしも一致しない)。
1884年にワシントンで開かれた万国子午線会議で、グリニッジ天文台の子午儀を通る子午線を地球の経度の基準である本初子午線(prime meridian)とすることが定められ、グリニッジは経度とともに世界の時刻の基準ともなった(世界時を参照)。
その後1948-58年にかけて、ロンドンの市街光を避けるため、天文台はグリニッジの南南東70kmにあるハーストモンソー城へ移転しRGO(Royal Greenwich Observatory)の名称となった。1967年には口径2.5mのアイザックニュートン望遠鏡(INT)を建設したが、1979年にINTはカナリー諸島のラパルマ島に移設された。グリニッジ天文台は、イギリス天文観測の新たな拠点として、この島のロークデロスムチャーチョス天文台に、口径4.2mのウィリアムハーシェル望遠鏡(WHT)を建設した。その後、1988-90年にかけて、RGOはハーストモンソー城からケンブリッジ大学構内に再移転し、国家的リストラが進む中1998年10月31日をもって、320年あまりの歴史に幕を閉じた。現在、グリニッジにある旧天文台の建物は博物館となっており、本初子午線は中庭にステンレス貼りの溝とレーザー光線で示されている。かつてRGOが行っていた保時・報時および航海暦の編集は、RGO閉鎖後、英国航海暦局(Her Majesty's Nautical Almanac Office)に引き継がれている。
参考ホームページ:
https://www.rmg.co.uk/discover/explore/royal-observatory-Greenwich
http://www.royalobservatorygreenwich.org/articles.php?article=0
宇宙の単位体積当たりの光度のこと。いわば宇宙空間の明るさである。光度には、(観測者が指定する)あるバンドにおける光度(正確には単位周波数当たりの光度)が用いられ、体積には共動体積が用いられる。ある赤方偏移における光度密度は、その赤方偏移での銀河の光度関数に光度を掛けて積分することで得られる。いろいろな波長で光度密度を求めれば、宇宙を満たす光のおおまかなスペクトルが描ける。
光度密度を視線方向に現在から過去まで(宇宙膨張の効果を考慮して)足し合わせると、宇宙背景放射が得られる。光度密度に似た量として、質量密度や星生成率密度などがある。
ウクライナにある天文台。ロシアの私設天文台をルーツとし、旧ソ連時代に、プルコボ天文台の観測所であった組織を1945年に改組して発足した。2.6 m, 1.25 m望遠鏡、太陽望遠鏡、ガンマ線望遠鏡などを有するほか、スペース天文学にも取り組んでいる。
ホームページ:https://www.crao.ru/en/
アメリカ合衆国アリゾナ大学のスチュワード天文台が運用する天文台の一つ。アリゾナ州グレアム山(標高3210m)にあり、大型双眼望遠鏡(スチュワード天文台)、ハインリッヒヘルツサブミリ波望遠鏡(アリゾナ大学アリゾナ電波天文台)、バチカン新技術望遠鏡(バチカン天文台)の3台の望遠鏡がある。グレアム山はアメリカ農林省の管轄するコロナド国立公園内にあり、入山には農林省林野部の許可が必要。
ホームページ:http://mgio.arizona.edu
アリゾナ州ツーソンに近いクウィンラン山頂(標高2096m)にある天文台。口径4 mのメイヨール望遠鏡(1973年の完成時には口径世界第2位)、WIYN 3.5 m望遠鏡、マクマスピアス太陽望遠鏡(世界最大の太陽望遠鏡)、など20台ほどの望遠鏡がある。アメリカ国立光学天文台のほか、いくつかの大学関係組織の施設により構成されている。
アメリカ国立光学天文台は2019年にアメリカ国立光学赤外線天文学研究所(NOIRLab)に発展改組された。
ホームページ: https://noirlab.edu/public/programs/kitt-peak-national-observatory/
NOIRLabに至る歴史
https://noirlab.edu/public/about/history-of-noao/
スペイン南部アンダルシア地方にある、ドイツとスペインによって共同運営されている天文台。ドイツのマックスプランク研究所と、スペインのアンダルシア天体物理研究所が運営主体である。1.23 m、2.2 m、3.5 mの3台の望遠鏡を共同利用に供している。
ホームページ:http://www.caha.es/
