関連画像
画像をクリックすると拡大されます

New
調べたい用語名の全部または一部を日本語または英語で入力してください。
日本語または英語で入力してください。
原子核が持つ量子力学的な角運動量のこと。原子核を構成する陽子と中性子の持つスピン角運動量と、それらが原子核内部で運動することに対応する角運動量とを合成した角運動量になる。電子などが磁気モーメントを持つのと同様に、原子核も […]
分子の回転準位間の遷移のこと。分子の回転のエネルギーは量子力学では量子化され、エネルギー固有値は回転量子数(角運動量の量子数)J やそれの回転対称軸への射影である K などで表される。これらの量子数の値によって異なるエネ […]
分子の回転エネルギーは量子力学では量子化されるが、そのエネルギー固有値である角運動量量子数のこと。記号 J で表す。一般には、その回転対称軸への射影を表す量子数 K と合わせて離散的なエネルギー準位が決まる。2つの異なる […]
系が平衡からずれた状態から平衡状態に近づく時間の目安を与える時間尺度。具体的には、平衡状態からのずれが指数関数的に減少する際の時定数。この場合、緩和時間が
ニュートン(I. Newton)の運動の第一法則(慣性の法則)が成り立つ座標系のこと。つまり、外力が働いていないか、働いている力が釣り合っている(合力が0)物体が、静止し続けるか等速直線運動となるような座標系である。慣性 […]
一般相対性理論において回転する重力源の周りの時空が遠方の慣性系に対して引きずられるように回転する効果。この効果のため回転する重力源に自由落下する観測者は無限遠で静止している観測者に対して回転方向に角速度を持つ。レンス-チ […]
ニュートン(I. Newton)の運動の第一法則(慣性の法則)が成り立つ座標系のこと。つまり、外力が働いていないか、働いている力が釣り合っている(合力が0)物体が、静止し続けるか等速直線運動となるような座標系である。慣性 […]
外力が働かないか、外力が中心力の場合、角運動量の値が一定のまま変化しないことを述べた法則。角運動量とは、天体の位置ベクトルを
光学的に厚い媒質中を光子が進む過程を拡散過程と近似し、媒質中の放射エネルギー流束を評価する近似法。光学的に厚い媒質中を光子が移動する場合、光子は媒質中をまっすぐに進むことができず、吸収・再放射・拡散を何度も繰り返し、媒質 […]
衝突が確率的に起こるとき、その粒子の運動は拡散過程で表現される。 一般に粒子の速度を
波長が約0.01 nmよりも短い電磁波(エネルギーでは約120 keV以上)の名称。波長域はX線と重なっている部分があるが、原子核の状態の遷移によって発生するものはガンマ線、電子のエネルギー状態の遷移によって発生するもの […]
慣性能率とも呼び、物体の回転しにくさを示す量である。たとえば、重さを無視できる棒の片方の端に回転軸があり、もう片方の端に質点と見なせる質量
原子核は陽子と中性子の集合体であるが、これらは必ずしもすべてが安定ではない。 不安定核が安定な核種になる過程には以下のものがある。 1.原子核中の中性子が電子と反電子ニュートリノを放出して陽子になる(ベータ崩壊) 2.原 […]
宇宙(銀河間空間)の電離度を推定する方法の一つ。ガン(J. Gunn)とピーターソン(B. Peterson)によって1965年に提案された。中性水素はライマンα(アルファ)線(静止系波長121.6 nm)の波長の光子を […]
宇宙はビッグバン以来膨張を続けている。宇宙膨張を支配するものが通常の重力であれば、物質の引き合う性質により膨張は必ず減速するはずである。しかし20世紀終わりに、遠方にあるIa型超新星の観測によって、実際には宇宙の膨張が加 […]
ゆらぎの統計的性質には無数の可能性があるが、そのうち特に簡単かつ一般的に現れやすい一群のゆらぎが、ガウスゆらぎと呼ばれる種類のものである。1変数のゆらぎに対しては、その分布関数がよく知られたガウス関数で表されるものがガウ […]
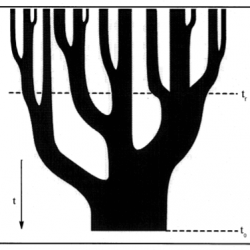
軽い銀河が最初に生まれ、それらが集合合体を繰り返して重い銀河や銀河の集団ができたとするモデル。われわれの宇宙のように冷たいダークマターが物質の大部分を占める宇宙では、銀河は必然的にこのように進化する。このモデルにおいて本 […]
画像をクリックすると拡大されます
