初期の宇宙では、光子とバリオン（通常の物質）が相互作用（トムソン散乱）で強く結合しており一つの流体として振る舞う。この光子バリオン流体は圧力を持つため、空間的な密度ゆらぎ（粗密）があると、それは音波振動となって空間を伝わってゆく。これをバリオン音響振動という。この日本語名称は松原隆彦氏による。英語名称（Baryon Acoustic Oscillation）の頭文字を取ってBAO（ビーエーオーと発音）と呼ばれることが多い。以下では簡単のためにBAOと表記する。ダークマターには圧力が働かないのでBAOは発生しない。

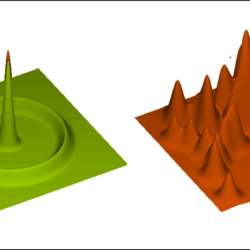
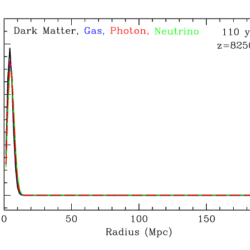
最初にバリオンの密度が高かったところでは光子バリオン流体の圧力が高く、そこから外向きの音波が発生して四方八方に広がる。二次元で例えれば、静かな水面に水滴を一つ落とした時に円形に波が広がるのに似ている（図1左）。この振動は宇宙の晴れ上がり時点までしか伝わることができない。宇宙の晴れ上がりが起きると光子とバリオンの相互作用が切れる（光子が脱結合する）ので振動はそのときの状態のまま止まる（凍結するともいう）。以後光子は空間を真っ直ぐに進む。最初に密度の高いところから放射された音波が宇宙の晴れ上がりまでに進んだ距離を音波の地平線（sound horizon；以下 $r_{\rm d}$）と呼ぶ（図1左の円周部）。初期の高密度部分を中心とする半径 $r_{\rm d}$ の球殻状の空間は、晴れ上がり時点でバリオンと光子の密度が少し高くなっている。これ以後は、バリオンのゆらぎとダークマターのゆらぎは重力不安定性によって成長し銀河などの天体ができる（図2）。晴れ上がり時点で出た光が真っ直ぐに宇宙空間を進んで我々に届いたものが宇宙マイクロ波背景放射である（図3）。

晴れ上がり時点の半径 $r_{\rm d}$ の球殻は宇宙膨張と共に引き延ばされ、後にできる銀河の分布（宇宙の大規模構造）にもこのパターンが刻み込まれる。実際の初期宇宙にはバリオンの高密度領域はさまざまな場所にさまざまな密度で存在するので、それぞれの場所から出る音波が重なり合って空間内に複雑なパターンを作り出す（図1 右）。このために特徴的なスケール $r_{\rm d}$（BAOピークもいう）を宇宙大規模構造のなかに目視で見つけることはできない。しかし、2点相関関数やパワースペクトルを精密に観測すればそれを検出し、その大きさを測定することができる（添付動画を参照）。

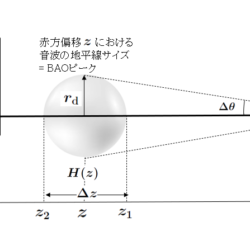
宇宙モデルを仮定すれば音波の地平線サイズ $r_{\rm d}$ は計算できる。このサイズは宇宙膨張と共に引き延ばされるが共動座標ではその長さは変わらない。したがって、これは宇宙における距離測定の「標準ものさし（standard ruler）」となる。大きさ一定の見えない球が宇宙空間のあちこちに浮かんでいると想像すると理解しやすい（図4）。

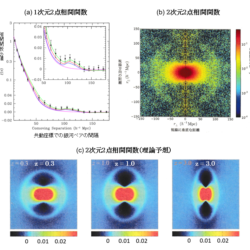
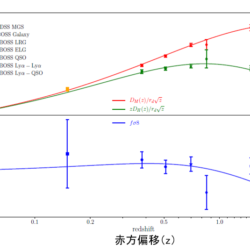
視線に垂直方向で（見かけの角度の）2点相関関数からBAOピークを測定すれば、それらの銀河までの角径距離（ $D_{\rm A}(z)=r_{\rm d}\Delta{\theta}$；図4参照 ）。また視線方向（赤方偏移）の2点相関関数からBAOピークを測定すれば、宇宙の膨張率を表すハッブルパラメータを $H(z)$として、図4より $H(z)=0.5c(z_2-z_1)/r_{\rm d}=0.5c\Delta{z}/r_{\rm d}$（ $c$ は光速度）となるので、$\Delta{z}$ の観測から銀河までのハッブル距離（ $D_{\rm H}(z)=c/H(z)$ ）が求まる。宇宙膨張の影響で、過去にさかのぼると両者は異なっており、さまざまな赤方偏移に対してこの観測をすれば、両者の赤方偏移依存性から宇宙膨張の歴史が分かる（図5,図6）。標準ものさしの長さは、ΛCDMモデルでは $H_0\sim70$ [km s^-1 Mpc^-1]なら共動座標で $r_{\rm d}\sim$150メガパーセク（Mpc）（約5億光年）である。

バリオン音響振動と銀河分布の関係を示す動画（CAASTRO, the new Centre of Excellence for All-sky Astrophysics）

https://www.youtube.com/embed/jpXuYc-wzk4?si=MVJBj-AXE4pKVHB3"