離心近点角

よみ方

りしんきんてんかく

英　語

eccentric anomaly

説　明

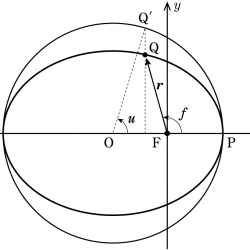
楕円軌道の焦点Fを原点に、近点Pから天体Qまで測った角度 $f$ を真近点角または真近点離角と呼ぶ。真近点角は物理的な実体を伴うので理解がしやすいが、数学的に扱うには不便な点もある。
そこで、楕円軌道に外接する円と、天体から焦点と近点を結ぶ線に対して下ろした垂線の延長が交わる点をQ'とし、外接円の中心Oを原点に、近点PからQ'まで測った角度 $u$ を定義し、これを離心近点角または離心近点離角と呼んでいる（図参照）。
たとえば、軌道長半径 $a$ 、離心率 $e$ の場合、天体の動径 $r$ は、真近点角 $f$ を使うと
$r=\frac{a(1-e^2)}{1+e\cos f}$
であるが、離心近点角 $u$ を用いれば
$r = a (1 - e \cos u)$
と簡単に書ける。