放射場と熱平衡状態にある物体の出す放射の放射強度（輝度）の周波数分布あるいは波長分布を表す法則。発見者であるドイツのプランク（Max Planck）にちなんでこの名前で呼ばれる。放射場と熱平衡状態にある物体の放出する電磁波を黒体放射と呼ぶため、プランクの黒体放射の法則とも呼ばれる。また、放射エネルギー分布（スペクトルエネルギー分布）そのものはプランク分布あるいはプランク関数と呼ばれる。プランク分布あるいはプランク関数をプランクの法則とよぶこともある。

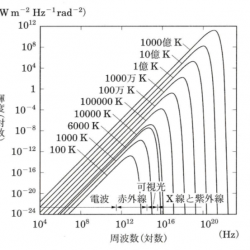
絶対温度  $T\,{\rm [K]}$ の黒体から放射される放射強度（単位時間、単位立体角あたり単位面積に到達するエネルギー）は、周波数 $\nu$ の関数として単位周波数あたりで表すと次の式で与えられる。

$$B_\nu(T)= \frac{2 h \nu^3}{c^2} \frac{1}
{{\rm exp}\, \left( \frac{h\nu} {k_{\rm B}T} \right) - 1}
\hspace{1cm}[{\rm J}\,\, {\rm s}^{-1}\,{\rm m}^{-2}\,{\rm Hz}^{-1}\,{\rm sr}^{-1}]\\\hspace{1cm}$$

ここで  $h$  はプランク定数、$k_{\rm B}$ はボルツマン定数、$c$ は光速度であり、[  ]内は単位を表す。これを単位波長あたりにして波長 $\lambda$ の関数で表すと次の式となる。

$$B_\lambda(T) =\frac{2hc^2}{\lambda^5} \frac{1}
{{\rm exp}\, \left(\frac{hc}{k_{\rm B}T\lambda} \right)-1}
\hspace{1cm}[{\rm J}\,{\rm s}^{-1}\,{\rm m}^{-2}\,{\rm m}^{-1}\,{\rm sr}^{-1}]\\\hspace{1cm}$$

ここで $c=\nu\lambda$ の関係がある。この $B_\nu(T)$ と $B_\lambda(T)$ をプランク分布あるいはプランク関数と呼ぶ（分光放射強度と呼ばれることもある）。

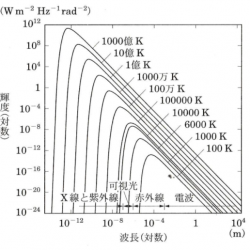
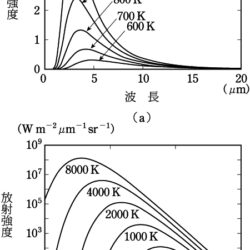
プランク分布あるいはプランク関数のグラフは、 $B_\nu(T)$ か $B_\lambda(T)$ のどちらを表しているのか、すなわち、横軸が周波数 $\nu$ か波長 $\lambda$ か、また、両軸の目盛が線形目盛か対数目盛かによって、見え方が大きく変わることに注意する。プランク分布 $B_\lambda(T)$ には最大となる波長 $\lambda_{\rm max}$ があり、その波長が絶対温度 $T$ に反比例することはプランク分布が理論的に確立する前から発見されており、ウィーンの変位則と呼ばれている。これを式で表すと次のようになる。

$$\lambda_{\rm max}=\frac{2.898\times10^{-3}}{T}\hspace{1cm}[{\rm m}]\hspace{1cm}$$

分光放射強度を全振動数あるいは全波長に渡って積分することで放射強度 $B\,(T)$ を求めることができる。すなわち、

$$\hspace{-3.5cm}B\,(T)=\int_0^\infty B_\nu(T){\rm d}\nu
= \int_0^\infty B_\lambda(T){\rm d}\lambda$$

$$\hspace{1cm}= \frac{2\pi^4k_{\rm B}^4}{15h^3c^2}T^4
\hspace{1cm}[{\rm J}\,{\rm s}^{-1}\,{\rm m}^{-2}\,{\rm sr}^{-1}]\,(=[{\rm W}\,{\rm m}^{-2}\,{\rm sr}^{-1}])\hspace{1cm}$$

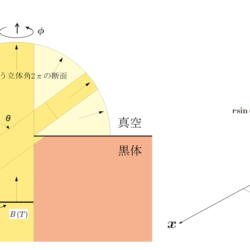
黒体の表面（単位面積）から前方のあらゆる方向に向かって単位時間に放射される全エネルギー $I\,(T)$ は、$B\,(T)$ を出射方向毎に重み ${\rm cos}\,\theta$（$\theta$ は表面に垂直な方向と出射方向とのなす角度）をつけて前方に向かう立体角 $2\pi$ に渡って積分した値となる。すなわち、

$$I\,(T)=\int_0^{2\pi}\int_0^{\frac{\pi}{2}}\,B\,(T)\,
{\rm cos}\,\theta\,{\rm sin}\,\theta\,{\rm d}\theta{\rm d}\phi=\pi{B\,(T)}\hspace{1cm}$$

ここで、

$$\frac{2\pi^5k_{\rm B}^4}{15h^3c^2}\equiv\sigma =5.67\times10^{-8}
\hspace{1cm}[W\,{\rm m}^{-2}\,{\rm K}^{-4}]\hspace{1cm}$$

と定義すると、

$$I\,(T)=\sigma\,{T}^4\,\,\,\,[{\rm J}\,{\rm s}^{-1}\,{\rm m}^{-2}] = [W\,{\rm m}^{-2}]\hspace{1cm}$$

となる。つまり $I\,(T)$ は温度 $T$ の4乗に比例する。これをシュテファン-ボルツマンの法則といい、比例定数 $\sigma$ はシュテファン-ボルツマン定数と呼ばれる。

分光放射強度から分光エネルギー密度を求めるには、分光放射強度を全立体角に渡って積分し、単位体積当たりに変換すればよい。すなわち、

$$u_\nu(T) = \frac{4\pi}{c}B_{\nu}(T)\hspace{1cm}[({\rm J}\,\, {\rm m}^{-3})\,{\rm Hz}^{-1}]\\\hspace{1cm}$$

$$u_\lambda(T) = \frac{4\pi}{c}B_{\lambda}(T)
\hspace{1cm}[({\rm J}\,\, {\rm m}^{-3})\,{\rm m}^{-1}]\\\hspace{1cm}$$

また、全エネルギー密度は次のようになる。、

$$u(T)=\int_0^\infty u_\nu(T){\rm d}\nu = \int_0^\infty u_\lambda(T){\rm d}\lambda
= \frac{8\pi^5}{15}\frac{(k_{\rm B}T)^4}{(hc)^3}\hspace{1cm}[{\rm J}\,\, {\rm m}^{-3}]\hspace{1cm}$$

プランクはこの法則の導出を考える過程で、黒体放射の入っている空洞壁の振動子のエネルギーが連続した値を取ることができず、$h\nu$（エネルギー量子）の整数倍になっていると仮定した。このエネルギーの量子仮説はその後の量子力学の発展に寄与した。