フェルミ統計
よみ方
ふぇるみとうけい
英 語
Fermi statistics
説 明
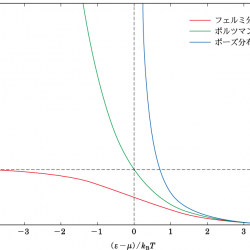
電子や中性子、ニュートリノなどフェルミ粒子の集団が従う統計規則。フェルミ分布あるいはフェルミ-ディラック分布ということもある。同一種類の複数のフェルミ粒子は区別がつかない。またパウリの排他原理により、同じ状態に複数の粒子は存在できない。このために温度 $T$ で熱平衡にある場合、状態 $i$ の分布関数は、
$$ f=\frac{1}{\exp[(\varepsilon_i-\mu)/k_{\rm B}T]+1} $$
と表される。ここで $\varepsilon_i$ は状態 $i$ のエネルギー準位、$\mu$ は化学ポテンシャル、$k_{\rm B}$ はボルツマン定数である。化学ポテンシャル $\mu$ が負の大きな数の場合、ボルツマン分布に近づく。化学ポテンシャルが基底状態のエネルギーより高く、温度が低い場合、縮退圧を発生させるようなフェルミ縮退という状態が実現する。ボース統計も参照。
2024年12月30日更新
この用語の改善に向けてご意見をお寄せください。
受信確認メール以外、個別のお返事は原則いたしませんのでご了解ください。