ウィーンの変位則
よみ方
うぃーんのへんいそく
英 語
Wien's displacement law
説 明
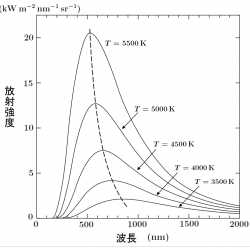
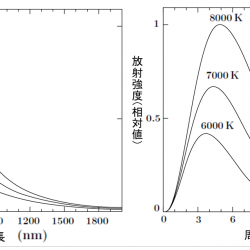
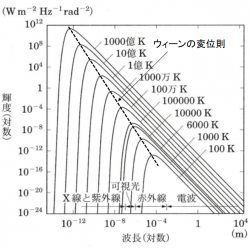
黒体放射のスペクトル(プランク分布)の最大エネルギーを与える波長 $\lambda_{\rm max}$ とその黒体の温度 $T$ の積(または最大エネルギーを与える振動数と黒体温度の比)は定数になるという法則。以下の式で表される。
$$\lambda_{\rm max}{T}=2.898\times10^{-3}\,\,\,\,[{\rm m\,K}]$$
波長の単位を[ $\mu {\rm m}$]にとると、
$$\lambda_{\rm max}\ [\mu {\rm m}]\ T\ [{\rm K}] = 2898 $$
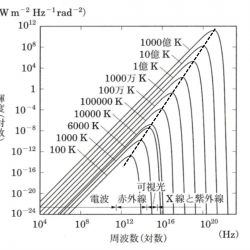
で表される。 このため、最大エネルギーとなる波長は黒体の温度が高いほど短波長になる。波長$1\,\mu {\rm m}$ でエネルギー最大となる放射スペクトルを持つ黒体の温度は 2898 K となる。太陽のスペクトルは波長約$0.5\,\mu {\rm m}$ 可視光で最大となっており、これより太陽の表面温度は約5800 Kであることがわかる。また、プランク分布を周波数 $\nu$ の関数で表した場合に、最大エネルギーを与える周波数 $\nu_{\rm max}$ は、
$$\nu_{\rm max}=5.879\times10^{10}\,T\,\,\,\,[{\rm Hz}]$$
となる。プランクの法則も参照。
2023年04月18日更新
この用語の改善に向けてご意見をお寄せください。
受信確認メール以外、個別のお返事は原則いたしませんのでご了解ください。