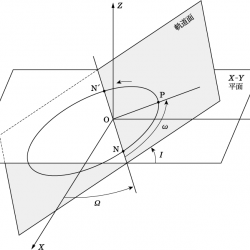
惑星など太陽の周りを回る天体の軌道や運動を表現するときに便利な量が軌道要素である。惑星などの場合、その軌道は近似的に楕円軌道となるが、軌道要素としては楕円の形を表す軌道長半径 $a$と 離心率$e$、楕円の空間での向きを示す軌道傾斜角 $I$、近日点引数 $\omega$、昇交点黄経 $\varOmega$、そして、近日点を通過する時刻である近日点通過時刻の6つの量を軌道要素として使うことが多い（図参照。Nは昇交点、Pは近日点、$e = \sqrt{1 – (b/a)^2}$、$b$ は軌道短半径）。これら6つの軌道要素は、その惑星の位置と速度の6つのパラメータと等価である。

天体の軌道を表す軌道要素は、二体問題を仮定すれば一定値をとるが、実際には摂動のために変動している。とくに瞬時の位置と速度から求めた軌道要素を接触軌道要素、短周期摂動による軌道要素の変化を取り除いたものを平均軌道要素と呼ぶ。惑星など、長期間にわたって軌道が安定している天体は平均軌道要素が便利であるが、軌道の不安定な小天体では接触軌道要素を用いるのが普通である。