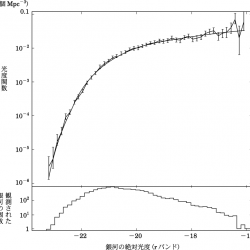
1976年にシェヒター（P.Schechter）によって提案された、銀河の光度関数を記述するための関数。 光度 にある銀河の数密度を として、

と表される。 ここで、は特徴的密度、は特徴的光度、は傾きと呼ばれる自由変数（パラメータ）であり、それらの値は、観測された光度関数を最もよく近似するように決める。 特徴的光度はシェヒター関数が屈曲する位置の光度に当たり、特徴的光度より明るい側では関数は指数関数的に減少し、暗い側ではべき関数的に増大する。 シェヒター関数は、階層的集団化モデルに登場するプレス-シェヒター理論の質量関数と似た関数形をしている。この事実は、階層的集団化モデルが本質において正しいことを示している。 全銀河の光度関数はシェヒター関数でかなりよく記述できるが、楕円銀河やレンズ状銀河の光度関数は釣鐘型をしているためシェヒター関数では表せない。