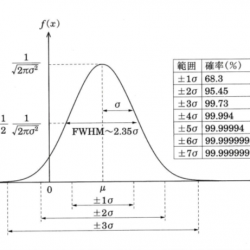
平均から外れるほど左右対称に確率が減少する「つりがね型」をした確率分布。ある集団の人間の身長の分布、多数の人が受験するテストの成績の分布、測定誤差の分布など、ほぼ正規分布に従う現象は、社会統計量や自然現象の中に多く存在する。正規分布は統計学の理論と応用において最も中心となるものである（図1）。

確率変数 $x$ に対する分布関数（確率密度関数）はガウス関数

$$ f(x;\mu,\sigma^2)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{-\frac{(x-\mu)^2}{2\sigma^2}\right\} $$

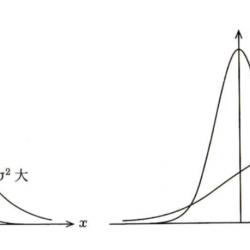
で与えられる。$f(x;\mu,\sigma^2)$ は $N(\mu, \sigma^2)$ と表記されることもある。天文分野では正規分布よりガウス分布（ガウシアン）と言われることが多い。ここで $\mu = \langle x \rangle$ は平均、$\sigma^2 =\langle (x-\mu)^2 \rangle$ は分散、$\sigma$ は標準偏差である。$\langle\,\,\rangle$ は中に示されている確率変数の期待値を示す。平均からのばらつきの度合い（つりがねの太さ）は分散で表されるが（図2左）、実際には変数と同じ単位を持つ標準偏差の方が多く用いられる。平均値 $\mu$ からのずれが $\pm \sigma$ 以内に収まる確率は68.27%、$\pm 2\sigma$ 以内に収まる確率は95.45%、$\pm 3\sigma$ 以内に収まる確率は99.73%である。

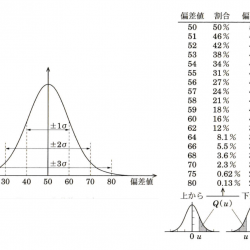
確率変数 $x$ を $u =(x -\mu)/\sigma$ と変換（標準化、正規化）すると、$u$ は平均値 0、分散 1の標準正規分布関数 $f(u;0,1)=N(0,1)$ に従う（図2右）。 逆に、標準正規分布関数を知れば、平均と分散が既知であるもとの変数の確率分布を知ることができる。このため多くの統計学の教科書には標準正規分布関数やその累積分布表がつけられている。今日では各種の計算ソフトによって標準正規分布は簡単に計算できる。学校教育現場でよく用いられる偏差値は、得点分布を平均50点、標準偏差10点の正規分布で近似したときの点数のことで、正規分布の性質から、集団内での自分の得点の位置を簡単に知ることができる（図3）。

正規分布は確率的な振る舞いをするいろいろな場面に現れやすい。その理由は中心極限定理と大数（たいすう）の法則にある。中心極限定理とは、多数の確率変数の和で与えられる一つの確率変数が、もとになった変数の確率分布によらず、正規分布に近づくという性質のことである。大数の法則とは、母集団から無作為に抽出された標本の平均は、標本数が大きくなると母集団の平均に近づくことを指す。サイコロを振って出る目の数を調べるような試行実験においては、「実験確率は試行回数を増やせば理論確率に近づく」とも表現される。N回サイコロを振って3の目が出る回数をn(3)とすると、n(3)/N は N が大きくなるほど1/6に近づく。正規分布は解析的取扱いが比較的容易であり、扱う問題に対して確率分布の正確な情報が得られないか、あるいは重要でない場合、正規分布が仮定されて用いられることが多い。実験データの解析の基礎である最小自乗法の基礎も正規分布にある。

ガウスは天文学の観測データの解析において、誤差が、ある関数（ガウスの誤差関数）に従うと仮定して誤差理論を完成させた。正規分布をガウス分布とも呼ぶのはこの誤差関数がガウス関数の基になっているからである。