相関係数

よみ方

そうかんけいすう

英　語

correlation coefficient

説　明

２つの確率変数 $x$ 、 $y$ のそれぞれの平均値 $x_0$ 、 $y_0$ とすると、２変数の平均値からのずれの積の期待値を、それぞれの変数の分散で除したもの、すなわち、
$r=\frac{E((x-x_0)(y-y_0))}{\sqrt{E((x-x_0)^2) E((y-y_0)^2)}}$
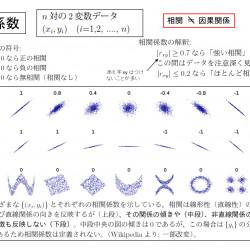
のことを相関係数という。ここで、関数 $E(z)$ は変数 $z$ の期待値。２変数が完全に相関している場合、両者の増減が一致していれば相関係数は+1に、増減が逆向きならば-1になり、無相関の場合には0になる。ただし、特殊な分布をしている場合にはなんらかの相関がある場合でも相関係数が0となることがある。
二つの変数の間に相関があってもそれは因果関係があることを直接意味するものではないことに注意が必要である。