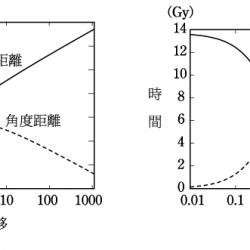
角径距離（角度距離、角直径距離ともいう）は、天体の実際の大きさと見かけの大きさの比にもとづいて定義される距離である。座標距離 $r$（赤方偏移 $z$）に大きさ $D$ の天体があり、その見かけの広がりが現在角度 $\Delta\theta$ に見えるとき、角径距離 $d_{\rm A}$ は $d_{\rm A}=D/\Delta\theta$ で定義される。ここで $D=a(t)\,r\Delta\theta$ なので、

$$d_{\rm A}=a(t)\,r=\frac{a_0\,r}{1+z}$$

となる。角径距離 $d_{\rm A}$ と光度距離 $d_{\rm L}$ の間には

$$d_{\rm L}=(1+z)^2\,d_{\rm A}$$

の関係がある。膨張宇宙で遠方の天体までの距離を測る場合、光が届く間にも宇宙は膨張していることに注意が必要である。角径距離と赤方偏移の対応については有用な諸データの表9を参照。
表9 https://astro-dic.jp/redshift-age-distance/