ラジアン

よみ方

らじあん

英　語

radian

説　明

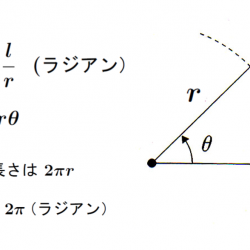
弧度法における角度の単位。半径 $r$ の円において長さ $l$ の円弧を見込む中心角が $\theta$ であるとき、 $\theta=l/r$ と定義するのが弧度法で、この角度の単位がラジアンである。半円周の長さは $l=\pi{r}$ なので、180度 $=\pi$ ラジアンである。テーラー展開などで用いられる微小角近似、 $\sin \theta\sim\theta$ などを使うときは角度の単位はラジアンでなければならない。
一般に用いられている角度の単位は度、分、秒である。角度の分と秒は時間の分と秒と同じ文字を使うので、両者の混同を避けるために角度を表す場合には角度分（または分角）、角度秒（または秒角）と表記することがある。度、（角度）分、（角度）秒とラジアンの変換は以下のとおり。
1度 $=\pi/180$ ラジアン、1（角度）分 $=\pi/(180\times 60)$ ラジアン、1（角度）秒 $=\pi/(180\times 60\times60)$ ラジアン
1ラジアン=57.296...度=3438（角度）分=2.0626 $\times 10^5$ （角度）秒。
天文学においては、距離 $r$ と天球上の見かけの大きさ $\theta$ から天体の真の大きさ $l$ を $l=r\theta$ として求めるので、角度のラジアン表記は重要である。また、天文学でよく使う距離の単位1パーセク（pc）は、1天文単位（au）を見込む角度が1（角度）秒になる距離と定義されているので、 $1\,{\rm pc}=2.0626\times10^5\,{\rm au}$ となる。角度表示も参照。