オールト定数
よみ方
おーるとていすう
英 語
Oort's constants
説 明
天の川銀河(銀河系)の回転に由来する、太陽系周辺の恒星の系統的な運動を表す式に登場する2つの定数のこと。オールト(J.H. Oort)が定式化したのでこの名前がついた。天の川銀河の円盤部のすべての天体が銀河中心の周りを円運動しているとし、その公転半径を $R$、公転速度を $\Theta$ としたときに
$$A=\left.\frac{1}{2} \left(\frac{\Theta}{R} – \frac{d\Theta}{dR}\right)\right|_{R=R_{0}}\\ \hspace{1cm}B=\left.-\frac{1}{2} \left(\frac{\Theta}{R}+\frac{d\Theta}{dR}\right)\right|_{R=R_{0}} $$
で定義される。ただし、$R_{0}, \Theta_{0}$ は太陽の位置での半径(銀河中心からの距離)と公転速度を表す。この定義から直ちに
$$A-B=\frac{\Theta_{0}}{R_{0}},\\\hspace{1cm} A+B=\left.-\frac{d\Theta}{dR}\right|_{R=R_{0}} $$
であることがわかる。 太陽を含むすべての恒星が天の川銀河の中心の周囲を円運動しているとすると、太陽系から銀経 $l$、距離 $D$ にある天体の視線速度 $v_r$ と接線方向速度 $v_t$</span) は
$$v_r=\left(\frac{\Theta}{R} – \frac{\Theta_{0}}{R_{0}}\right)R_{0} \sin l, \\ \hspace{1cm}v_t=\left(\frac{\Theta}{R} – \frac{\Theta_{0}}{R_{0}}\right)R_{0} \cos l- \frac{\Theta}{R}D $$
となる。この式を $D \ll R_{0}$, $D \ll R$, $|R-R_{0}| \ll R_{0}$ の場合に1次近似すると、先に示したオールト定数 $A, B$ を用いて
$$ v_r=AD \sin 2l,\quad\\ v_t=(A \cos 2l + B)D $$
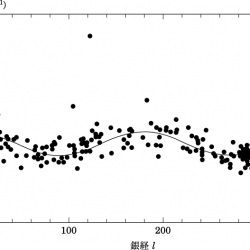
となる。後者はさらに $ \frac{v_t}{D}=A \cos 2l + B $ と変形でき、この左辺は固有運動の銀経方向成分である。
実際の恒星の運動には円運動からのずれがあるが、多数の恒星に対する観測によってそれを平均化できると仮定し、いろいろな銀経方向で様々な距離にある星の運動の観測からこの式に当てはまるパターンが見つかったことで銀河回転の証拠となった。また、その値から、$\Theta_0$ や $R_0$ が観測的に求められる。
2023年04月18日更新
この用語の改善に向けてご意見をお寄せください。
受信確認メール以外、個別のお返事は原則いたしませんのでご了解ください。