ルジャンドル多項式

よみ方

るじゃんどるたこうしき

英　語

Legendre polynomials

説　明

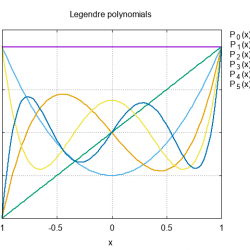
重力ポテンシャルのような $1/r$ の形を持つ関数を展開するときに現れる多項式のこと。
具体的には
$P_n(x)=\frac{1}{2^nn!}\frac{d^n}{dx^n}(x^2-1)^n$
と書ける。たとえば、
$P_0(x)=1,$
$P_1(x)=x,$
$P_2(x)=\frac{3x^2-1}{2}$
である。漸化式
$(n+1)P_{n+1}(x)-(2n+1)xP_n(x)+nP_{n-1}(x)=0$
あるいは
$nP_n(x)=x\frac{dP_n}{dx}-\frac{dP_{n-1}}{dx}$
から求めることもできる。