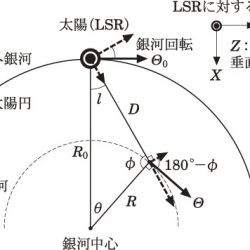
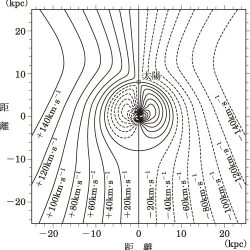
天の川銀河（銀河系）の回転運動を利用して、天の川銀河の円盤に属する天体までの距離を視線速度に基づいて求めたもの。天の川銀河の円盤部は、銀河中心の周りをほぼ円運動している。この運動は差動回転であるため、太陽系から見たある方向の視線速度は距離の関数となり、以下の式で表される。

$$ v_r=\left(\frac{\Theta}{R}-\frac{\Theta_{0}}{R_{0}}\right)R_{0} \sin l $$

ここで、 $R, \Theta$ は天の川 銀河中心からの距離と回転速度、$l$ は銀経を示し、添え字0は 太陽（厳密には、局所静止基準）に対する値であることを示す。これと、余弦定理から得られる、

$$ D=R_0 \cos l \pm \sqrt{R^2 – R_0^2 \sin^2 l} $$

を組み合わせると、視線速度 $v_r$ と運動学的距離 $D$ との関係式を得ることができる。式中に複号が現れることからもわかるように、運動に対称性があるため、銀河中心からの距離が太陽系よりも近い天体については同じ視線速度となる距離が2つになるので、このような天体については運動学的距離が一意に決まらない。これを遠近問題と呼ぶ。また、天の川銀河中心方向およびその反対方向については視線速度が常に0になるため、測定誤差も考慮に入れると、この2つの方向に近い方向では運動学的距離を決めることができない。さらに、個々の天体の固有運動や実際の銀河回転が仮定している円運動から系統的にずれているなどの理由によって、個々の天体に対する距離としては数割程度の誤差があるといわれているが、上記の理由により実際の精度は天の川銀河内の場所によって大きく異なる。これらの欠点はあるものの、天の川銀河内の天体の大局的な分布を普遍的に知るには最も有力な距離決定方法である。